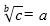Premio Emma Castelnuovo

Premio Emma Castelnuovo

La Potenciación

Una aclaratoria con base en lo señalado en la pág. 184 de la décima lección del libro de segundo año de la colección Bicentenario.

El profesor de Matemática, cuando trabaja las lecciones que tienen que ver o están relacionadas con o necesitan usar las operaciones aritméticas debe tener claro tres aspectos:

1)   La Definición Matemática de las Operaciones Aritméticas desde la matemática como Ciencia

2)   Los Modelos de las Operaciones Aritméticas que se enseñan

3)   Los Algoritmos de las Operaciones Aritméticas

Recordemos que la adición se define como una función f:AxAàA  con A perteneciente a un conjunto numérico cualquiera (N, Z, Q, R o C) donde f(a+b)=c  con a, b, c pertenecientes a un conjunto numérico A; de igual manera se definen el resto de funciones con las restricciones del caso de acuerdo al conjunto numérico en el que se esté trabajando.

Los modelos didácticos usados para la comprensión de las operaciones deben proporcionar elementos, desde la matemática, que contribuyan a la formación de los conceptos adecuados.

Es por ello, que, por ejemplo, la adición repetida en la educación secundaria o media general sería poco útil para el estudio de estas operaciones en los conjuntos Q, R y C. Es mucho más enriquecedor el modelo de área o plano cartesiano, tal como se usa en la página 102 y 103 de la sexta lección del libro de primer año de la colección Bicentenario.

Ahora bien, si se desea estudiar las propiedades de la potenciación, como de cualquier otra operación, se deben estudiar y analizar de manera conjunta la operación y su operación inversa, noción esta que será de utilidad en el álgebra, despeje de ecuaciones e inecuaciones.

Esto, además, debido a que todo proceso de la vida real, que se pueda analizar o modelar con matemática, se le puede definir su proceso en reversa, para ello es importante comprender la relación entre las operaciones con el fin de poder enriquecer el análisis de cualquier proceso que se estudie: almacenaje, inventarios, insumos, crecimiento poblacional y un largo etc.

Por ejemplo, ingreso o salida de insumos o combinación de insumos para la preparación de productos en una fábrica de alimentos

Proceso (operación)	Proceso Inverso (Operación Inversa)
Adición	Sustracción
operación que permite calcular el valor de la suma	operación que permite calcular el valor de un sumando
Si se usan 2,25Kg de guayaba y medio kilo de azúcar,  ¿cuántos kilos de concentrado de guayaba se obtienen?	Para preparar 2,75 kilos de concentrado de guayaba, si se usan dos kilos y un cuarto de guayabas, ¿cuántos kilos de azúcar se requieren?

Por ejemplo, análisis de movilización de pasajeros en funiculares

Proceso (operación)	Proceso Inverso (Operación Inversa)
Multiplicación	División
operación que permite calcular el valor del producto	operación que permite calcular el valor de un factor
6x8=48	48÷6=8
Si seis funiculares en una hora pico viajan llenos, ¿cuántos pasajeros transportan?	Si se trasladan hasta Hornos de Cal 48 pasajeros y los funiculares viajaron siempre con seis pasajeros, ¿cuántos funiculares se usaron para el traslado?

Por ejemplo, análisis de crecimiento poblacional

 donde a es la base; n el exponente y b la potencia

Acá debemos recordar que la potenciación tiene dos operaciones inversas

Operación	Operación inversa
Potenciación	Radicación
	operación que permite calcular el valor de la base
operación que permite calcular el valor de la potencia	Logaritmización
	operación que permite calcular el valor del exponente

Proceso (operación)	Proceso Inverso (Operación Inversa)
Potenciación	logaritmización
El crecimiento de una población de Drosophila melanogaster, también llamada  mosca de la fruta, se puede modelar con la función f(x)=2x, ¿cuántos elementos se estima que tendrá dicha población en determinado espacio al cabo de 5 meses?	Si en un almacén de frutas se establece que la población de Drosophila melanogaster no puede exceder el número de 32 individuos por metro cúbico, ¿cada cuánto tiempo se debe fumigar para controlar la población de insectos?

Propiedades de la Potenciación y Logaritmización

 Completa la tabla con las otras propiedades

De lo Real a lo Formal en Matemática

Artículos para el debate Pedagógico

De lo Real a lo Formal en Matemática

(Integra Educativa Vol. III/N°2)

Darwin Silva

(UPEL-IPC)

Introducción

Es impostergable el desarrollo de una educación matemática vinculada a las realidades de nuestra patria latinoamericana. Para ello, se hace necesario superar la enseñanza basada exclusivamente en pasos y algoritmos completamente descontextualizados y, avanzar hacia la producción de ideas matemáticas basadas en el estudio de fenómenos naturales o sociales, donde la capacidad de abstracción es necesaria pero sin perder jamás de vista la tierra firme.

La matemática, con sus conceptos, procedimientos, técnicas y representaciones, aporta elementos para la comprensión y la transformación de la realidad, mientras que esta misma realidad, a su vez, ofrece fenómenos naturales y sociales que permiten la producción de ideas matemáticas.

El proceso de enseñar y aprender matemática debe fundarse en metodologías formativas con base en la realidad experimental de la vida escolar y comunitaria, donde se promueva el trabajo cooperativo y en equipo, se favorezca el desarrollo de capacidades para la resolución de problemas, se impulse la concepción interdisciplinar de las ciencias, se vincule el aprendizaje con los medios de producción material y se potencie la integración afectiva y social de los responsables.

Apoyados en lo anterior y convencidos como estamos de que la educación venezolana debe ser transformada, presentamos nuestro trabajo, el cual esperamos sea de utilidad para nuestras y nuestros compañeros docentes de matemática interesados en comprender y cambiar el estado actual de la educación matemática en nuestros países latinoamericanos.

Educación, Matemática y Sociedad

¿Por qué y para qué debe educarse a los habitantes de una nación?, ¿será acaso para domesticarlos y hacerlos cumplir, de manera irreflexiva, cada una de las ordenes de la clase dominante?, ¿ tiene sentido un proceso educativo apartado de la vida, centrado en la palabra sin sentido y preocupado, casi exclusivamente, por los procesos económicos?, ¿podemos construir una patria verdaderamente democrática con una educación no acostumbrada al diálogo, apartada de la investigación y sin amor por el estudio?

Las preguntas anteriores no son de sencillo abordaje, ante todo porque las respuestas que se puede ofrecer son muchas. Por lo tanto, en las líneas siguientes presentaremos lo mencionado en distintas fuentes sobre los puntos centrales de las interrogantes anteriores.

En el artículo 15, numeral dos de la Ley Orgánica de Educación (2009) venezolana, se establece como uno de los fines de la educación el siguiente:

Desarrollar una nueva cultura política fundamentada en la participación protagónica y el fortalecimiento del Poder Popular, en la democratización del saber y en la promoción de la escuela como espacio de formación de ciudadanía y de participación comunitaria, para la reconstrucción del espíritu público en los nuevos republicanos y en las nuevas republicanas con profunda conciencia del deber social.

A partir de lo anterior, podemos decir que la educación debe permitir que el hombre y la mujer participen en los procesos de transformación social; dichas transformaciones deben siempre responder a los intereses de las mayorías y nunca a los de las clases económicamente dominantes e históricamente opresoras, pero sin dejar de reconocer los derechos que los miembros de estas ostentan como seres humanos. Para ello, es necesario avanzar hacia la formación de un ser critico y apto para 1 convivir en una sociedad democrática; para Skovsmose (1999: 16) ser crítico significa prestarle atención a una situación crítica, identificarla, tratar de captarla, comprenderla y reaccionar frente a ella. Ser crítico se refiere en parte a ser analítico ante cualquier situación, pero además, la idea de crítica está enmarcada en la necesidad de producir cambios y esclarecer las contradicciones presentes en nuestras sociedades. Skovsmose (1999: 11) afirma que mientras crítica y educación se mantengan separadas, la segunda fácilmente puede tomar la forma de una entrega de información, o la función de socializar a la juventud dentro de la cultura existente.

La educación debe ser el proceso mediante el cual el individuo aprenda y comprenda los valores y tradiciones de su cultura, para comprender su sociedad y ser capaz de transformarla. De acuerdo con Barreiro (1975, citado en Freire, 1975: 14),

La alfabetización, y por ende toda la tarea de educar, sólo será auténticamente humanista en la medida en que procure la integración del individuo a su realidad nacional, en la medida en que le pierda miedo a la libertad, en la medida en que pueda crear en el educando un proceso de recreación, de búsqueda, de independencia y, a la vez, de solidaridad.

La educación debe contribuir a alcanzar una sociedad más democrática y participativa, donde cada persona encuentre las condiciones y oportunidades para su liberación. La escuela tiene que enseñar a los estudiantes a practicar, apreciar y defender valores básicos como el amor patrio, la equidad, la democracia, la fraternidad y la tolerancia.

Según Freire (1975: 92),

La democracia y la educación democrática se fundan en la creencia del hombre, en la creencia de que ellas no sólo pueden sino que deben discutir sus problemas, el problema de su país, de su continente, del mundo, los problemas de su trabajo, los problemas de la propia democracia.

La escuela no puede continuar maravillada por la sonoridad de la palabra, por la memorización de los fragmentos, por la desvinculación de la realidad, por la tendencia a reducir los medios de aprendizaje afirmas meramente nacionales (: 57), lo cual sin duda no es más que una posición ingenua de nuestras sociedades latinoamericanas.

El ciudadano común debe ser capaz de comprender, analizar, utilizar y transformar el orden económico, cultural, social, político, ambiental, científico y tecnológico imperante en su sociedad. Pero esto es imposible si la ciencia en general y la matemática en particular, son vistas solamente como un conjunto de ejecuciones aisladas, donde en muchos casos no se ofrece ninguna imagen, ni siquiera parcial o limitada, del mundo.

Es necesario que nuestros estudiantes al, estudiar matemáticas, sientan que están estudiando un mundo real, donde los fenómenos sociales, políticos, económicos y culturales son considerados al momento de indagar, experimentar, errar, discutir, maravillar, dudar, crear, aplicar, generalizar, abstraer y formalizar.

Es importante que las y los estudiantes y también las y los profesores reconozcan que el conocimiento matemático se puede producir a partir de actos creativos e imaginativos, vinculados con métodos de búsqueda científica. Según De Guzmán (1993: 6), la matemática es, sobre todo, saber hacer, es una ciencia en la que el método claramente predomina sobre el contenido; esta afirmación permite vincular la enseñanza de la matemática a la resolución de problemas, los cuales deben tener como contexto el mundo político, económico y social en el cual están inmersos los y las estudiantes.

El proceso de aprender y enseñar matemáticas debe estar vinculado a la vida cotidiana de los actores del proceso, lo que significa que la matemática debe estar al servicio del entorno cultural, social, político, económico y natural.

...los problemas del mundo real serán usados para desarrollar conceptos matemáticos..., luego habrá ocasión de abstraer, a diferentes niveles, de formalizar y generalizar... y volver a aplicar lo aprendido..., y reinventar la matemática (De Lange, 1986, citado en Alsina s/fi 8).

Una educación matemática vinculada a la realidad, es sin duda una tarea interesante y compleja. El método de proyectos y la modelación son dos importantes concepciones didácticas que hacen viable el binomio matemática-realidad.

El Método de Proyectos

El método de proyectos tiene sus inicios a mediados del siglo XVII, cuando se funda en París la Academia Real. En dicha institución los estudiantes, para poder culminar los estudios de arquitectura, debían presentar un trabajo práctico vinculado a un problema de diseño para una construcción (Knoll, 1997).

En Venezuela, las primeras referencias vinculadas al método de proyectos las podemos encontrar dentro del marco de la Escuela Nueva. Para el año 1933, la Educación Primaria contaba con nuevos programas, y en ellos podemos encontrar algunas pequeñas referencias a principios y métodos de la escuela activa. El método de proyectos es incorporado en los programas de urbanidad e higiene a partir del 3er grado.

El año 1997, con la reformas de las primeras dos etapas de Educación Básica, el método de proyectos es introducido como estrategia de planificación central del currículo. De esta manera surgen el Proyecto Pedagógico de Plantel (PPP) y el Proyecto Pedagógico de Aula (PPA).

La experiencia más reciente con el método de proyectos, en nuestro país, está la relacionada con el Proyecto Educativo Integral Comunitario (PEIC), el Proyecto de Aprendizaje (PA) y el Proyecto de Desarrollo Endógeno, propuestos por el Sistema Educativo Bolivariano como una manera de organizar la gestión escolar a partir de la investigación de situaciones reales de la vida diaria y la participación integrada de todos los actores del proceso educativo (Ministerio del Poder Popular Para la Educación, 2007: 66).

El Sistema Educativo Bolivariano propone los proyectos como una forma de organización de los aprendizajes, pero, ¿en qué consiste el método de trabajo por proyectos?

Según Mora (2004: 114), podemos definir el método de proyectos Lomo una búsqueda organizada de respuestas, por parte del trabajo cooperativo entre estudiantes, docentes, padres, a un conjunto de interrogantes en torno a un problema o tema relevante desde el punto de vista social, individual y colectivo. Los proyectos educativos representan una forma de organización escolar que propone estudiar la realidad para intervenir en ella.

En el mismo orden de ideas, Aravena y Jiménez (2002) mencionan, con respecto a los proyectos, que:

-       Contribuyen al desarrollo de la autonomía. Este es un concepto clave en la forma de aprendizaje que se basa en la reflexión sobre la propia experiencia.

-       Ayudan al desarrollo de la motivación. La relación entre motivación y aprendizaje desempeña un papel crucial en el trabajo por proyectos.

-       Estimulan el uso de capacidades cognitivas y metacognitivas en las y los estudiantes.

-       Favorecen, en la formación del estudiante, la capacidad para enfrentarse con flexibilidad y confianza a problemas nuevos y complejos, en un mundo que está en cambio permanente.

-       Reflejan una integración de los contenidos aprendidos y permiten reconocer y mejorar concepciones del estudiante sobre el propio papel del contenido matemático como ayuda a la modelación, promoviendo un proceso de regulación importante.

Según Schulz (1973 y 1980, citado en Mora, 2004: 31), una unidad basada en proyectos debe estar constituida por las siguientes características:

1.    Un proyecto de enseñanza debe partir de las necesidades de las y los estudiantes.

2.    Dominio de situaciones concretas de la vida, las cuales no solamente están inmersas en ci mundo cerrado de la escuela, sino aquellas que sean relevantes precisamente en la realidad cotidiana.

3.    Orientado hacia la producción no solamente del conocimiento intelectual, sino además la producción y uso de tecnología en la elaboración de cosas útiles para el mismo aprendizaje y para beneficio de los estudiantes.

4.    Superación de la frontera entre el tratamiento de las especificidades inherentes a cada disciplina científica, lo cual significa enseñanza basada en la interdisciplinariedad.

5.    La enseñanza orientada en proyectos debe ser socialmente relevante y significativa para todos los individuos.

6.    Este tipo de enseñanza requiere del trabajo en grupos.

La educación guiada por la metodología de trabajo por proyectos pareciera ser sumamente ambiciosa por lo que, tal vez, se ha ganado muchas enemistades y ha suscitado una gran desconfianza entre quienes defienden el trabajo disciplinar y especializado de los conocimientos científicos. Se dice que los proyectos son poco sistemáticos, lo que, para algunos, no beneficia el aprendizaje de conocimientos vinculados con las ciencias naturales y las matemáticas. Otros aseguran que la educación por proyectos beneficia la formación integral y crítica de las personas. Nuestra intención es determinar el grado de veracidad de esas afirmaciones a través de la práctica social.

Con respecto a la elección de los temas y contenidos de un proyecto, Mora (2004: 41) nos dice que un proyecto, en sentido estricto, debe permitir que las y los estudiantes determinen los temas y contenidos. Nosotros consideramos dos variantes de esta propuesta inicial: la primera deja que las y los estudiantes y profesores fijen en conjunto los temas de trabajo; y la segunda permite que los estudiantes escojan los temas a partir de una presentación previa, que debe ser bastante variada, efectuada por los profesores. Es importante señalar que Mora no considera como un proyecto aquel en que el docente impone el tema sin tomar en cuenta la opinión de los estudiantes.

Por su parte, Skovsmose (1999) no considera este último punto como una condición indispensable del método de proyectos. Las condiciones establecidas por este autor son las siguientes: a) el tema tiene que ser bastante conocido para los educandos, la situación escogida debe poderse formular y discutir en el lenguaje natural; b) los educandos deben poder desarrollar el tema aún si sus habilidades fuesen bastante diferentes entre sí; c) el tema debe poseer un valor por sí mismo, no debe convertirse en una mera introducción a una parte de una nueva teoría matemática o de alguna otra área del conocimiento; d) el trabajo debe crear conceptos matemáticos, físicos, biológicos, sociales, culturales, etc., así como también debe procurar que el estudiante identifique dónde y cómo aplicar o usar ideas matemáticas, físicas, biológicas, etc.

Con respecto a cómo decidir cuáles serán los objetivos del trabajo, Mora (2004) plantea tres posibilidades: a) las y los estudiantes, de manera independiente, formulan problemas y objetivos; b) las y los estudiantes y las y los profesores deciden los objetivos conjuntamente; c) las y los estudiantes escogen algunos objetivos de entre los presentados por la o el profesor. Si bien es necesario establecer unos objetivos iniciales que guíen el desarrollo del proyecto, también es importante atender los problemas y objetivos no considerados en la planificación inicial. Estas nuevas situaciones pueden ser abordadas en el desarrollo del mismo proyecto, o pueden ser el punto de partida de uno nuevo.

Otro elemento importante que se debe considerar durante la realización de proyectos educativos, es la evaluación. Generalmente, evaluar es una actividad poco amigable, de hecho pareciera ser más interesante desarrollar un proyecto que evaluarlo, lo que en ocasiones no es nada sencillo. Pero, a pesar de todo esto, no es concebible un proyecto educativo sin una evaluación y esto se debe a que este proceso permite determinar: a) el grado de desarrollo del proyecto; b) si es necesaria una reorientación; c) cuáles son los procesos y productos logrados por los estudiantes; d) a qué necesidades y a qué contexto responde el proyecto; y e) cuál es el desenvolvimiento de los participantes.

Cuando se habla de evaluación de los aprendizajes generalmente se hace referencia a dos modalidades: la formativa y la sumativa. Refiriéndose al tema de los proyectos, Abrantes, P., Bastos, R., Brunheira, L. y da Ponte,J. (1998: 24) afirman que:

…la evaluación formativa se realiza en cualquier punto del proceso y tiene por objetivo verificar como andan las cosas..., la evaluación sumativa corresponde al balance final que se hace sobre un proyecto, inventariando la calidad de sus productos y aprendizajes.

No podemos evaluar un proyecto educativo mediante una prueba de tiempo fijo, es importante que el(los) encargado(s) del proceso evaluativo documente(n), empezando en el mismo momento en que se elige el problema desde la revisión bibliográfica, el diseño de la investigación y la descripción del modelo, hasta la entrega del informe final.

La información que se debe registrar y cómo hacerlo, de seguro estará determinada en gran medida por las creencias del docente y las particularidades individuales y colectivas de los grupos de trabajo. Sin embargo, creemos importante que, durante la ejecución del proyecto, en lo que a matemática se refiere, se registren: datos cognitivos (producción de conocimientos matemáticos), epistemológicos (connotaciones matemática-realidad) y heurísticos (estrategias utilizadas en la resolución del problema) (Fortuny y Gómez, 2002).

Por otra parte, consideramos necesario registrar las características socio-afectivas (motivación, participación, capacidad comunicativa) de todo el estudiantado que toman parte en las diferentes etapas del proyecto.

La evaluación debe ser un proceso que permita mejorar profundamente la enseñanza y el aprendizaje de la matemática, así como también una manera de registrar y analizar información relevante que permita conocer qué, cómo, cuándo y cuánto aprenden los educandos.

Ya para finalizar, un elemento que puede hacer viable la enseñanza de la matemática basada en el método de proyectos, es el de la modelación, cuyo punto de partida es el planteamiento de un problema que puede provenir de la matemática o del mundo real.

Modelación Matemática

Una forma de esquematizar el proceso de modelación planteado por D’ Ambrosio (1985), se puede evidenciar en el gráfico 1 que presentamos a continuación:

Gráfico 1. Modelación matemática

Fuente: D’Ambrosio (1985)

El esquema expuesto en este gráfico está diseñado de tal manera que se comience con un problema que provenga de la realidad. La experiencia educativa de una o un estudiante estará incompleta mientras no tenga ocasión de resolver problemas que estén vinculados con su localidad, región o país y que, además, sean de interés para la comunidad. En un primer momento, es normal que exista un enunciado vago de lo que se quiere, será a partir del análisis y de la investigación de los elementos vinculados con la situación real que se enunciará el problema con todo detalle. Las situaciones realistas deben contener informaciones ricas en contenidos para las y los estudiantes, incluir diversas interrogantes, incorporar diferentes áreas del conocimiento científico y permitir el tratamiento de amplios y variados contenidos matemáticos. Las situaciones problemáticas prácticas tomadas de la realidad siempre deben ser mostradas en forma de tareas verbales.

Las y los estudiantes deben construir el modelo matemático de la tarea expresada de forma verbal. No es lo mismo contar desde el principio con el modelo, que elaborarlo. La misión de construcción no es sencilla. En este momento, lo que se realiza es la sustitución de palabras por símbolos propios de la especificidad matemática (ecuaciones, inecuaciones, relaciones, funciones, etc.). Fortuny y Gómez (2002: 9) mencionan al respecto lo siguiente: De esta forma se consigue una formulación matemática del problema y, de una manera natural, se establece el problema en términos matemáticos.

Normalmente, las y los estudiantes tienen problemas para resolver modelos matemáticos (Fortuny y Gómez, 2002; Orellana, 2004). Es preciso resolver el modelo usando las herramientas adecuadas. Por ello, es importante auto-regular y controlar las decisiones globales referidas a la implementación de recursos y estrategias.

Resulta importante que el estudiante se dé cuenta de que, para llegar a resolver un problema usual de su ámbito social, necesita del aprendizaje de conceptos, términos, definiciones, procedimientos y algoritmos propios del saber matemático que proporcionen respuestas al modelo establecido. De esta manera, el alumno alcanza un grado fuertemente elevado de interés por el aprendizaje de las matemáticas, ya que visualiza su utilidad (Fortuny y Gómez, 2002: 9). Un estudiante motivado estará en condiciones de empezar a desarrollar su independencia cognitiva. Es importante acotar que, en este trabajo, el desarrollo de procesos mentales es entendido principal, aunque no exclusivamente, como un medio para la compresión y transformación de las estructuras sociales en crisis.

Por último, es necesario interpretar y reescribir los resultados numéricos obtenidos en términos del problema propuesto y, también, saber escoger, si hay diferentes soluciones, la más adecuada al problema real inicial.

Habilidades Matemáticas

En los años 70 comenzó a surgir, entre los educadores matemáticos, fuerte reacción contra la existencia de un currículo único y la forma impuesta de presentar la matemática en todos los países. La matemática moderna, con la sustitución de buena parte de la geometría por el álgebra, convirtió a la matemática escolar en puras generalidades sobre conjuntos y lógica, dejando de lado temas y problemas muy interesantes. Además, esta reforma no dejaba espacio a la valorización del conocimiento que la niña y el niño trae hacia la escuela.

Después del fracaso, desde el punto de vista de la enseñanza, de la matemática moderna, ha surgido en el mundo una gran discusión en torno a cuáles matemáticas se debe enseñar y de qué manera se debe enseñarlas.

Con respecto a este asunto, De Guzmán (1993: 5) afirma que:

La filosofía de la matemática actual ha dejado de preocuparse tan insistentemente como en la primera parte del siglo sobre los problemas de fundamentación de la matemática, para enfocar su atención en el carácter cuasi empírico de la actividad matemática (1. Lakatos), así como en los aspectos relativos a la historicidad e inmersión de la matemática en la cultura de la sociedad en la que se origina (R. L. Wilder)

En su obra Pruebas y Refutaciones. La lógica del descubrimiento matemático (1978), Lakatos postula que la matemática deben ser desarrolladas siguiendo ci patrón de las conjeturas, las pruebas y las refutaciones.

Según Gazcón (s/f), el punto de partida para este patrón debe ser un problema (no necesariamente matemático) en el que la atención se fija en los momentos más oscuros e informales de la teoría matemática en elaboración. Lo más importante, desde esta postura, son los procedimientos (no necesariamente algorítmicos): conjeturar, probar, contrastar, refutar, buscar contraejemplos, comparar con problemas similares, etc. Bajo este punto de vista, las matemáticas dejan de ser un conjunto de verdades eternas, infalibles, sagradas, dogmáticas y se convierten en una manifestación humana que se vale de los argumentos por analogía, del significado físico de algunos conceptos, del mundo real, de la intuición, la deducción, el análisis, la síntesis, la particularidad, la generalidad y la lógica para su conformación y evolución.

Es necesario motivar a los y las estudiantes para que reflexionen sobre sus pensamientos y actividades. Las situaciones problemáticas deben permitir que los educandos no se limiten a buscar la respuesta correcta, sino que traten de hallar las razones por las cuales un procedimiento, algoritmo o teorema eso no útil para la resolución del problema estudiado.

Tall (1991) caracteriza al pensamiento matemático a través de procesos como la clasificación, la representación, la deducción, la abstracción, la visualización, la generalización y la demostración. Este autor advierte que estos no son los únicos procesos presentes al momento de pensar matemáticamente. Cantoral (2000) se aproxima a la definición de pensamiento matemático, comparándolo con las formas en las que piensan los matemáticos profesionales.

Habilidades de pensamiento como particularizar, generalizar, conjeturar, argumentar, analizar, clasificar, sintetizar y explicar deben ser una referencia para cualquier programa que se interese por presentar a las matemáticas como una manera de conocer y rehacer e1 mundo real.

Una educación matemática preocupada por desarrollar en los estudiantes habilidades matemáticas que les permitan comprender y participar de manera activa en su entorno y entender la matemática como un sistema, debe considerar los elementos expuestos por Lakatos y Tall, pero además es necesario que se interese por estudiar los problemas de la matemática como disciplina científica, su desarrollo histórico, la veracidad de las proposiciones y por reflexionar entorno a preguntas como:

¿De qué manera la matemática contribuye a la comprensión de fenómenos sociales y naturales?, ¿qué tan próximos a la realidad son los resultados arrojados por un análisis matemático?, ¿se hubiese podido llegar a una conclusión similar sin matemáticas?, ¿el mundo exterior a las matemáticas aporta elementos para su desarrollo?, ¿ se puede prescindir de las técnicas matemáticas a la hora de resolver un modelo matemático?, ¿la enseñanza de la matemática responde a intereses políticos y económicos?, ¿las matemáticas son una manera de legitimar la desigualdad educativa? Una enseñanza de la matemática y de las ciencias naturales vinculada con situaciones problemáticas reales y significativas para la sociedad y, por lo tanto, para las y los estudiantes, ¿puede contribuir a un cambio en las condiciones materiales de producción y al desarrollo de la conciencia de los ciudadanos venezolanos? Los y las estudiantes de nuestra educación media, ¿están preparados cognitiva, física y emocionalmente para el estudio del mundo real, que es su mundo?

Las preguntas anteriores son fáciles de formular, pero difíciles de responder científicamente y la única manera de contestar correctamente es participando en la práctica que modifica la realidad.

Si realmente existe un interés por alcanzar una enseñanza de la matemática vinculada a la comprensión y transformación de situaciones en crisis, es necesario aprovechar el marco conceptual de las matemáticas y el de las ciencias naturales para obtener una interpretación específica de un modelo de la realidad, para que, posteriormente, las mismas matemáticas, las ciencias naturales y la tecnología desarrollen e incorporen modelos que contribuyan a intervenir en la realidad.

Una experiencia de investigación-acción crítica basada en el método de proyectos

Toda investigación responde al enfoque, modelo conceptual o paradigma que se asuma, lo cual condicionará los procedimientos que se desarrollen en la misma. Cada enfoque tiene una conceptualización diferente de cómo, qué, para qué, dónde y por qué investigar. En nuestro caso, asumimos como enfoque de investigación el paradigma sociocrítico, que parte de supuestos emancipatorios y se vale de la investigación para comprender e intervenir en la realidad.

Para Carr y Kemmis (1988), bajo el marco de una Ciencia Social Crítica, la relación entre lo teórico y lo práctico no puede limitarse exclusivamente a prescribir una práctica en base a una teoría, ni a informar el juicio práctico. Para estos autores, la teoría debe ser el resultado de un proceso llevado a cabo por una persona o grupo con el fin de entender sus propias prácticas, así como las situaciones en que se realizan.

Con base en lo anterior, se hace indispensable una investigación educativa que se ocupe del mejoramiento de las prácticas, de la comprensión de las mismas y de las situaciones en que se llevan a cabo, para hallar la nueva educación a través de la crítica de la antigua.

Según Mckernan (2001: 47), la investigación-acción crítica se ve como un proceso que da poder político a los participantes; la lucha es por formas más racionales, justas y democráticas de educación. No es suficiente que unos pocos expertos se encarguen de investigar externamente la educación, con el fin de producir teorías educativas que luego serán puestas en práctica por las y los profesionales en ejercicio, lo cual crea una insalvable separación entre la teoría y la práctica; es necesario que el currículo se alimente de la investigación realizada por los docentes dentro de la escuela, se debe respetar el derecho que tienen las profesoras y los profesores de adquirir y producir conocimientos a partir de la reflexión sobre su práctica. Además, se debe reivindicar a la escuela como el centro de la investigación educativa.

En esta investigación, nos interesamos por reflexionar, analizar y describir los datos que emergiesen de la interacción entre los estudiantes, el profesor, las situaciones problemáticas y las matemáticas, con la intención de intervenir en la realidad del estudiante, del profesor y en el diseño curricular de las matemáticas escolares.

A través de este trabajo hemos aportado elementos que permitirán desarrollar unas matemáticas escolares que sean útiles para la comprensión y transformación de situaciones en crisis y, por ello, deseamos desarrollar en las y los estudiantes habilidades matemáticas tales como la reflexión, la argumentación, la visualización, la representación y la formalización, a partir del estudio de algún fenómeno proveniente del mundo real.

Los sujetos involucrados en esta investigación fueron:

-       25 estudiantes de tercer año de Educación Media, estudiantes de la Unidad Educativa Nacional General José Francisco Bermúdez, la cual está ubicada en la comunidad de El Rodeo, en el estado Miranda.

-       El docente del curso, Magister en Educación Mención Enseñanza de la Matemática, con siete años de experiencia docente.

Presentación y Análisis de los Resultados

A continuación presentamos algunos de los análisis crítico- reflexivos elaborados a partir de ¡os diarios, los talleres escritos, las pruebas escritas y los cuadernos de cinco estudiantes de tercer año de educación media que participaron en el desarrollo de los proyectos educativos, que tenían como tema generador La valoración de las distintas fuentes de energía. A partir de lo establecido por Becerra (2006) y Moya (2008), en nuestra investigación omitimos los nombres y el género de las y los estudiantes participantes, que serán identificados desde Estudiante 1 (El) hasta Estudiante 5 (E 5).

La información está organizada en categorías, que son una especie de etiquetas creadas para agrupar la información vinculada entre sí, respetando la naturaleza de la misma.

Categoría 1: Concepto de función

Esta categoría se refiere a las formas en la que los estudiantes producen y se apropian del concepto de función. En el gráfico 2, se observa lo dicho por las y los estudiantes sobre este importante concepto de la matemática.

Gráfico 2

Categoría: Concepto de función

En el comentario aportado por el Estudiante 2, podemos observar que el establecimiento de variables y la representación gráfica de la relación establecida entre ellas no resultó ser una actividad sencilla, esto se evidencia en la cita [2:23] [101] Dígame para expresar la relación en un gráfico, eso sí que fue bastante complicada; la relación a la que hace referencia el Estudiante 2 es la que viene dada por las variables Kilovatios! hora (Kw/h.) y costo en bolívares (Bs.), sobre datos tomados de una factura emitida por Electricidad de Caracas. Lo importante aquí es observar cómo, a partir de un recibo de luz y de la necesidad que tiene el estudiante de conocer qué características tiene el consumo de energía eléctrica en su hogar, comienza a producir elementos vinculados con la matemática; en este caso, se apoya en una representación gráfica de tipo cartesiana que le permite comprender la situación planteada. Además, la representación en el plano cartesiano no aparece como resultado de un procedimiento mecánico de construcción punto a punto, sino que es una construcción con una intencionalidad, que consiste en representar una situación de una forma particular.

El Estudiante 2 continúa diciendo en la cita [2:24] [103]: …después teníamos que decir si esa gráfica definía una función o no, eso sí que era bastante fácil; en este caso, el estudiante utilizó, como se observa en la fi gura 1, el criterio de la línea vertical (cualquier recta de ecuación x = a, con a Î R, que corte a la curva en uno y sólo en un punto) para justificar que la gráfica define una función.

Figura 1

Taller escrito 2

En la figura 1 podemos observar cómo los estudiantes, a partir de los datos analizados en cada uno de los proyectos, se apoyan en representaciones, procedimientos y conceptos matemáticos que les permiten interpretar la situación problemática planteada. El Estudiante 3 afirma que [3:19] [72]...ya que, para que pueda decir que es función, es necesario que cada elemento de °C  esté relacionado con un único elemento de °F; en este caso, utiliza un sistema de tipo verbal para justificar que la relación es una función. Consideramos importante señalar que no es conveniente hablar de un sólo registro representativo para algunos conceptos cuya naturaleza admite la posibilidad de diferentes representaciones, lo que nos permite hablar de sistemas de representación (Vernaugd, 1990).

La consideración exclusiva y absoluta de un modo de representación puede obstaculizar la plena comprensión del concepto. Según Bagni (2004), el concepto defunción se vincula, a menudo, directamente con la gráfica cartesiana de la relación examinada; para muchos alumnos tal conexión es esencial para decidir si una relación es una función. El autor afirma a continuación que:

…tal situación, intuitiva y didácticamente importante, debe ser controlada por el profesor, una exagerada presentación visual podría llevar a los alumnos a malos entendidos a propósito del carácter de algunas relaciones que no se considerarían funciones en cuanto no pueden visualizarse como curvas.

En la figura 2 se puede ver cómo uno de las y los estudiantes representa la relación Kw/h-Bs. de distintas maneras y se apoya en ellas para justificar que la relación define una función. AL estudiar este concepto, es importante considerar diferentes formas de representación, tales como: la descripción verbal, el modelo físico, la tabla de valores, el diagrama de Venn, el gráfico cartesiano y las fórmulas o ecuaciones, de manera que la diversidad de representaciones permita al estudiante una mejor comprensión del objeto representado.

Figura 2

Taller escrito 2

El Estudiante 2 nos dice, en la cita [2:22] [89], que esa clase sí que era difícil, dígame cuando nos mandaron a explicar, eso si no lo realicé del tiro por lo difícil que era. Bueno, sólo explicarlo, porque de representarlo eso sí que es fácil, hicimos representaciones. En este punto el estudiante expresa claramente que tiene dificultad para realizar la explicación de un hecho en matemáticas, lo que se debe a: 1) que explicar no es una actividad común dentro del aula de matemáticas, generalmente los estudiantes realizan unos cuantos ejercicios de forma mecánica, pero sin enterarse del por qué y el para qué de esta actividad, a lo que se ha denominado paradigma del ejercicio (Skovsmose, 1999); y 2) que explicar está vinculado al por qué de las cosas, lo cual es una actividad cognitivamente exigente. Bishop nos dice que explicar es una actividad que conduce al desarrollo de las matemáticas, y la considera como la actividad que eleva la cognición humana por encima del nivel asociado a la mera experiencia del entorno (1999: 71).

Observemos cómo el Estudiante 1 [1:37] [76] se preocupa por explicar lo que para él significa punto medio de un segmento: Vimos cómo determinar el punto medio de un segmento de varias formas, 1era) sumando el punto de un lado del segmento + el otro punto del otro lado del segmento entre dos, lo que nos diera era el punto medio de x segmento; 2da) viendo cuál es la distancia que hay entre un punto y otro, esa distancia la dividimos entre dos y ese es punta medio de x segmento. El estudiante, al explicar cómo se calcula el punto medio de un segmento, produce un algoritmo que le será útil en futuras tareas.

Además, menciona algunos atributos de este concepto, lo que le permite ir apropiándose de esta idea matemática; de acuerdo con Skovsmose (2000), el significado también puede verse, primero que todo, coma una característica de las acciones y no sólo de los conceptos. Para este autor, haber escuchado la definición conceptual no garantiza la comprensión del concepto. Según Vinner (1991), adquirir un concepto significa tener una imagen conceptual de él. En esta investigación, intentamos resolver el problema de la comprensión conceptual planteando situaciones a ser analizadas por medio de procedimientos, representaciones y conceptos de la matemática que los estudiantes debían aprender cómo y cuándo utilizar.

Para aproximarnos de mejor manera al significado que le han asignado los estudiantes a este concepto, analicemos lo realizado por ellos en uno de los talleres escritos.

Figura 3

Taller escrito 1

En la figura 3 podemos observar cómo se establece la relación entre las escalas Fahrenheit y Kelvin considerando sus equivalentes; para ello, se utiliza un concepto geométrico como el de punto medio, lo cual ofrece la posibilidad de que los estudiantes reconozcan la conexión que hay entre las distintas áreas de las matemáticas (Geometría- Álgebra) y que se beneficien de la comprensión de cómo se ha establecido la relación entre las variables.

Categoría 2: Papel del estudiante

Para la conformación de esta categoría, hemos utilizado los comentarios realizados por el Estudiante 2 en su diario de clase, los cuales hacen referencia a un aspecto del papel que les corresponde tomar a los educandos durante el desarrollo de los proyectos educativos. Estas opiniones están reseñadas en el gráfico 3.

El Estudiante 2, en la cita [2:17] [176], refiriéndose a unos comentarios realizados por el profesor del curso durante el desarrollo de una de las actividades de los proyectos, indica: se lo dije que no hablara con ese tono, que bajara más la voz, porque asustaba a uno, entonces pone nervioso a uno. Y bajó la voz y todo se normalizó, y agrega en la cita [2:15] [168] pero hasta lo irrespetuosa se me quería salir, es que provocaba lanzarle la regla que tenía para que dejara la criticadera y el quejar, pero como yo sé que son críticas constructivas, no me molestó.

Gráfico 3

Categoría: Papel del estudiante

De las afirmaciones anteriores, podemos deducir que el estudiante está inconforme con el comportamiento del docente, lo que despierta en él la necesidad de reclamar un mejor trato, pero no lo hace de una forma irrespetuosa, sino que enfrenta la situación y al docente con argumentos que le hacen comprender al docente que su actitud no está beneficiando el proceso de aprendizaje de las y los estudiantes.

Bajo una estructura clásica de la escuela, el profesor o la profesora son la máxima instancia de poder y autoridad dentro del espacio de aprendizaje, lo que lo o la convierte en una figura que no puede ser cuestionada. Esta corriente considera que los y las estudiantes son meros receptores de la acción docente, lo que entra en plena contradicción con una educación democrática y participativa, donde las y los estudiantes tienen derecho a expresar sus ideas en torno a qué aprender y cómo aprenderlo.

Es cierto que, dentro del marco de una enseñanza de la matemática guiada por la metodología de trabajo por proyectos, el líder debe seguir siendo el docente, pero esto no quiere decir que sus decisiones y acciones no puedan ser cuestionadas por las y los estudiantes, o que no puedan existir líderes entre ellos que contribuyan a un mejor desarrollo del proceso de enseñanza-aprendizaje.

Es indispensable que la escuela enseñe a las y los educandos a enfrentar, de forma colectiva, legal, justa, consciente y sin importar la estructura de poder que los sustente, a cualquier acto o persona que vulnere valores y derechos como el respeto, la libertad, la vida, la libre expresión, el acceso a la educación, a la salud, a la vivienda, a la recreación, al transporte público, etc. Para ello, es indispensable que nuestras y nuestros estudiantes posean conocimientos científico-tecnológicos y que estén en la creencia de que pueden participar productivamente en su proceso educativo y en la formación de una patria mejor.

Con base en lo anterior, se hace necesario tener mucho cuidado de que, con el pretexto de garantizar la prosecución escolar, nuestros y nuestras estudiantes avancen en el sistema educativo sin obtener los conocimientos necesarios que les permitan analizar fenómenos naturales o comprender, criticar y transformar las situaciones de crisis que se presentan en su medio social; no podemos entregarles a la razón universal o a una ética carente de hechos, información y conciencia, negándoles la posibilidad de juzgar, participar y transformar el mundo, del que cada uno de nosotros es parte.

Es indispensable generar en los educan dos el compromiso y amor por aprender, en esto los y las docentes jugamos un papel fundamental. En nuestro caso particular, si bien es cierto que en algunos momentos nos equivocábamos en la forma de guiar el proceso de enseñanza-aprendizaje, tal como lo expresa el estudiante 2, nos agrada saber que los estudiantes no se detuvieron en su responsabilidad de aprender, lo cual se evidencia en la cita [2:16] [170] del Estudiante 2, quien comenta: dije, ‘tenlo por seguro que ésta no se la paso, ya va a ver lo que voy a hacer, le voy a estudiar hasta lo que no vimos para que quede boquiabierto’ y continúa diciendo, en la cita [2:14] [174], que me la descobré, le hice la exposición bien, le dije hasta lo que no estudiamos. Y dijo que estaba bien.

Algunos dirán que la motivación del estudiante por aprender se origina en un sentimiento de revancha contra el profesor, pero nos atrevemos a asegurar, apoyados en todas las citas presentadas y en los documentos completos que reflejan las opiniones del Estudiante 2, que este estilo de escribir es una forma de expresar su compromiso con todas las actividades del proyecto, sus compañeras, compañeros y docente.

Conclusiones

A continuación presentamos un conjunto de consideraciones finales que pretenden dar cuenta de los hallazgos de este estudio. Esperamos que, a partir de ellos, se continúe desarrollando otras investigaciones que permitan la transformación del proceso de enseñanza-aprendizaje de la matemática correspondiente al nivel de educación media.

Aprendizajes vinculados con el concepto de función: las y los estudiantes, a partir de la necesidad que tienen de conocer las características de las situaciones planteadas en cada uno de los proyectos, por ejemplo el comportamiento que tiene el consumo de energía en su hogar, comienzan a generar representaciones, procedimientos e ideas matemáticas de manera contextualizada e intencional. De esta forma, cuestiones como representar gráficamente funciones, calcular la distancia entre dos puntos o determinar el punto medio de un segmento no son el resultado de un procedimiento mecánico.

Los educandos hacen uso de diferentes representaciones gráficas, tales como la descripción verbal, la tabla de valores, el diagrama de Venn, el gráfico cartesiano y las formulas o ecuaciones, para interpretarla situación planteada pero, además, las diversas representaciones permiten visualizar las características del concepto.

A lo largo de desarrollo del proyecto La energía en la casa, los estudiantes se dan cuenta de la necesidad de utilizar procedimientos matemáticos que les permitan ir analizando la situación no matemática, el contexto extra-matemático funciona como una forma de representación de los conceptos matemáticos.

Papel del estudiante: a medida que el desarrollo de los proyectos avanzaba, el grado de compromiso de los y las estudiantes era mayor, ellos y ellas se convirtieron, cada vez más, en los protagonistas de las experiencias de aprendizaje, aportaban ideas relacionadas con el tema abordado y, aunque existieron ciertas dificultades, se preocupaban por tener los materiales necesarios para el desarrollo de las actividades. A pesar de la poca tradición de trabajar en equipo, colaboraban entre si durante el desarrollo de cada uno de los proyectos, lo que no significó que alguien realizara el trabajo correspondiente a otro compañero o compañera.

También lograron  superar la barrera impuesta por nuestra educación, el no confrontar con argumentos los excesos y las faltas del profesor. En una educación democrática y participativa, los y las estudiantes tienen derecho a enfrentar cualquier instancia de poder que vulnere sus derechos.

Bibliografía Consultada

Abrantes, P. Bastos, R. Brunheira, L. y DaPonte, J. (1998). Matemática. Proyectos Educativos. Lisboa: Editorial do Ministério de Educação.

Alsina, C. (s/f). Geometría y Realidad. Disponible en: http://wwwupc. es/ea-smi/pcrsonal/claudi/documents/geometria_realidad.pdf [Consultado el 20 de abril de 2006].

Aravena, M. y Jiménez, J. (2002). Evaluación de procesos de modelización polinómica mediante proyectos. Uno Revista de Didáctica de las matemáticas. No 31.

Bagni, G. (2004). Una experiencia didáctica sobre funciones en la escuela secundaria. Revista Latinoamericana de Investigación en Matemática Educativa. Vol. 7, N° 1.

Becerra, R. (2006). La formación del docente integrador bajo un enfoque interdisciplinario y transformador Desde la perspectiva de los Grupos Profesionales en Educación Matemática. Tesis Doctoral no publicada. Caracas: universidad Pedagógica Experimental Libertador. Instituto Pedagógico de Caracas.

Bishop, A. (1999). Enculturación matemática. La educación matemática desde una perspectiva cultural. Barcelona: Paidós.

Cantoral, R (coord.) (2000). Desarrollo del pensamiento matemático. México: Trillas.

Carr, W. y Kemmis, S. (1988). Teoría crítica de la enseñanza. La investigación-acción en la formación del profesorado. Barcelona: Martínez Roca.

D’Ambrosio, U. (1985). Aspectos sociológicos de la Enseñanza de la Matemática. Vol. 3. España: Thales.

De Guzmán, M. (1993). Tendencias innovadoras en educación matemática. Disponible en: http: //ww.mat.ucm.es/deptos/am/guzman/tendencia/ ensen.httnlntroducción [Consultado ci 10 de junio de 2006].

Fortuny, J. y Gómez, J. (2002). Contribución al estudio de los procesos de modelización en la enseñanza de las matemáticas en las escuelas universitarias. Uno Revista de Didáctica de las matemáticas. N. 31. Freire, P. 1975. La educación como práctica de la libertad. México: Siglo XXI.

Gazcón, J. (s/f). Incidencia del modelo epistemológico de las matemáticas sobre las prácticas docentes. Disponible en: http://exa.unne.edu.ar/ grado/carreras_a_termino/documentos! Gascon_Relime.pdf [Consultado el 14 de junio de 2007].

Knoll, M. (1997). The Project method: Its vocational education origin and international development. Journal of Industrial Teacher Education, 34(3). Disponible en: http://scholar.lib.vt.edu/ejournalsI JITE/v34n3/ Knoll.html

Lakatos, I. (1978). Pruebas y Refutaciones. La lógica del descubrimiento matemático. Madrid: Alianza universidad.

Gaceta Oficial de la República Bolivariana de Venezuela No 5.929 Extraordinaria. (2009). Ley Orgánica de Educación.

Mckernan, J. (2001). Investigación-acción y Currículo. Madrid: Morata.

Mora, D. (2004). “Aspectos pedagógicos y didácticos sobre el método de proyectos”. En: Mora, D. (ed.) Tópicos en educación matemática. Caracas: Grupo de Investigación y Difusión sobre Educación Matemática.

Ministerio del Poder Popular Para la Educación. (2007). Currículo Nacional Bolivariano. Diseño Curricular del Sistema Educativo Bolivariano. Caracas: Autor.

Moya, A. (2008). Elementos para la construcción de un modelo de evaluación en matemática para el nivel de educación superior. Tesis Doctoral no publicada, universidad Pedagógica Experimental Libertador. Instituto Pedagógico de Miranda José Manuel Siso Martínez.

Orellana, M. (2004). Modelos matemáticos como estrategia de enseñanza-aprendizaje y una historia breve de la matemática aplicada. Seminario sobre Modelos y Modelado: Conceptos, técnicas y aplicaciones universidad Fermín Toro, auspiciado por la Comisión de Estudios Interdisciplinarios de la universidad Central de Venezuela.

Skovsmose, O. (1999). Hacia una filosofía de la educación matemática crítica. Bogotá: Una Empresa Docente.

Skovsmose, O. (2000). Escenarios de investigación. Revista EMA. N° 6.

Tall, D. (ed.) (1991). Advanced mathematical thinking. Holanda: Kluwer Academic.

Vinner, S. (1991). “The role of definitions in the teaching and learning of mathematics” En: Tall, D. (cd.) Advanced Mathematical Thinking. Holanda: Kluwer Academic.

Vernaugd, G. (1990). La teoría de los campos conceptuales. Investigaciones en Didáctica de las Matemáticas. 10 (23).